Generating polynomial:
If reference signal or disturbance signal
satisfy differential equation as:
Then, taking
Laplace Transform
:
where
is a polynomial in
series because of initial conditions
.
We call
disturbance
generating polynomial
.
-> Examples:
|
|
|
|
|
(constant)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 1. Laplace transform and Generating polynomial
For a fundamental review of IMP (Internal Model Principle), see
[exercise]
Internal Model Principle:
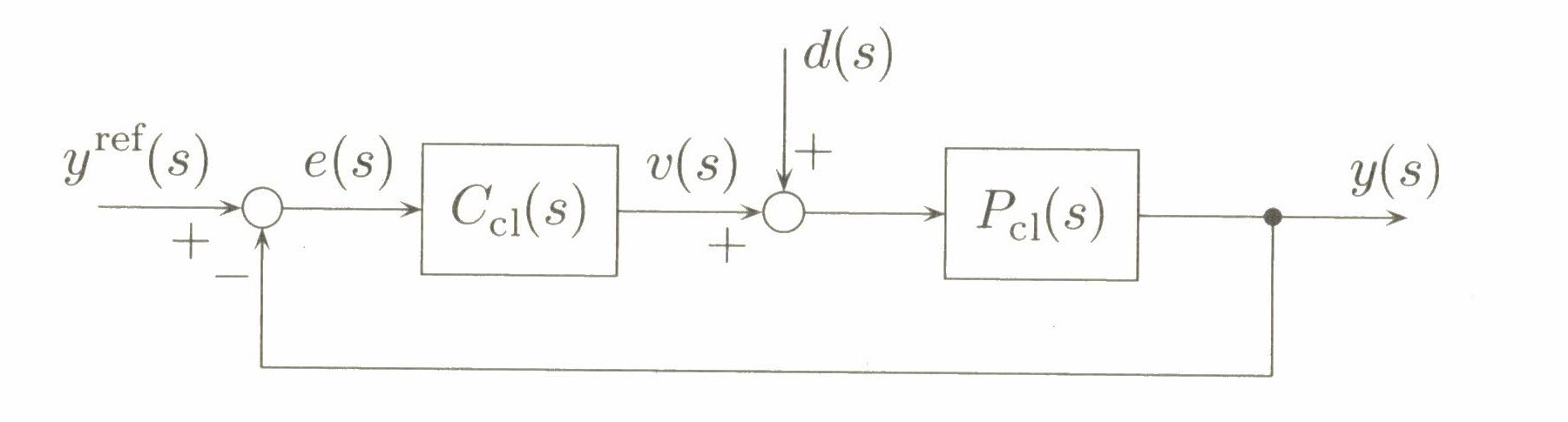
Figure 2.1 feedback control system
[ref]
If disturbance
and reference
as is shown in
Figure 2.1
both have
as the
generating polynomial
, then using a controller of the form:
in the standard
one degree-of-freedom control
architecture can
asymptotically
reject the effect of the disturbance and cause the output to track the reference.
-> Derivation:
Let the plant model
in
Figure 2.1
be
, assume
is not a factor of
.
Figure 2.2 Diagram of
(a)
sensitivity
; (b)
input sensitivity
; (c)
complementary sensitivity
.
The
sensitivity
function
, a.k.a. the transfer function between an output disturbance and output as is shown in
Figure 2.2(a)
, the
input sensitivity
function
, a.k.a. the transfer function between an intput disturbance and output as is shown in
Figure 2.2(b)
, the
complementary sensitivity
function
, a.k.a. the transfer function between the reference input and the output as is shown in
Figure 2.2(c)
, are obtained as:
Suppose that
and
have been designed to have all the roots of
closed loop characteristic equation
is negative in real parts. The response of the system to the output disturbance
with
generating polynomial
is:
Similarily, the response of the system to the input disturbance
and the response of the system to the reference input may be derived as also. Notice
may has non-negative roots in real parts, still
has all roots' real parts in negative domain. Then
.
-> Exercise: Input signal is time-delayed (
)

Figure 2.3 Control input time delayed
Transfer function:
Error function:
