5.1 フィードフォワードを利用した目標値追従制御
5.1.1 定値の目標値への追従制御
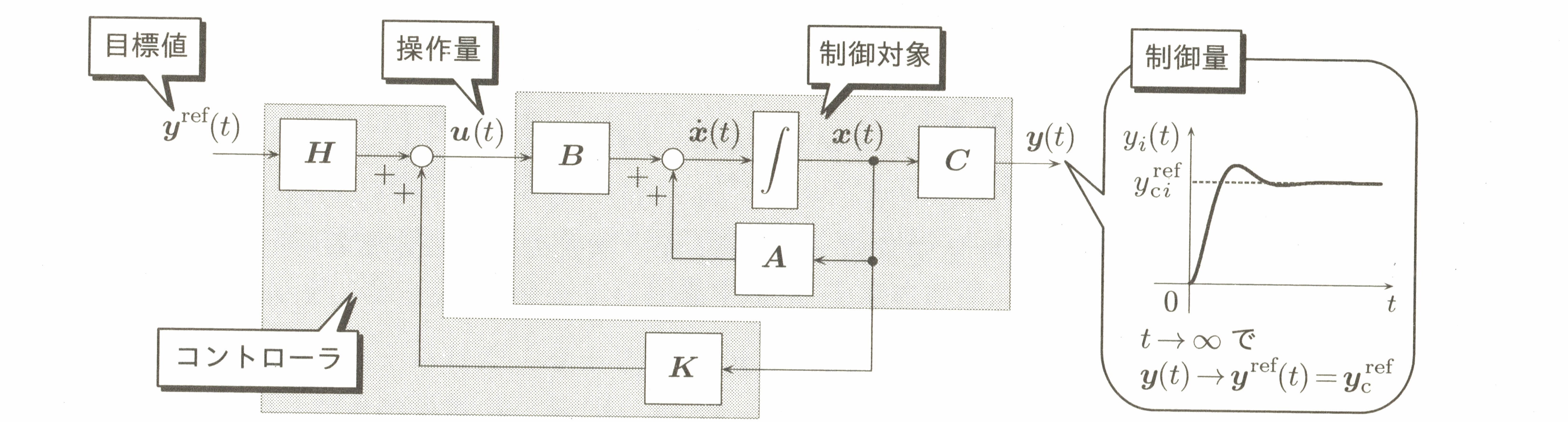
Figure 5.1 track control using feedforwad
稳态条件:
当 时,由 式(5.1) 得,
式(5.1) 减去 式(5.5) 得,
如果按此种方法设计, 时,有
其中, ,即
得
Theorem 5.1:
Extra: Iterative control
discrete condition
ILC
objective and final state condition
error
differential
control rule
5.2 サーボシステムと積分型コントローラ
5.2.1 サーボシステムと内部モデル原理
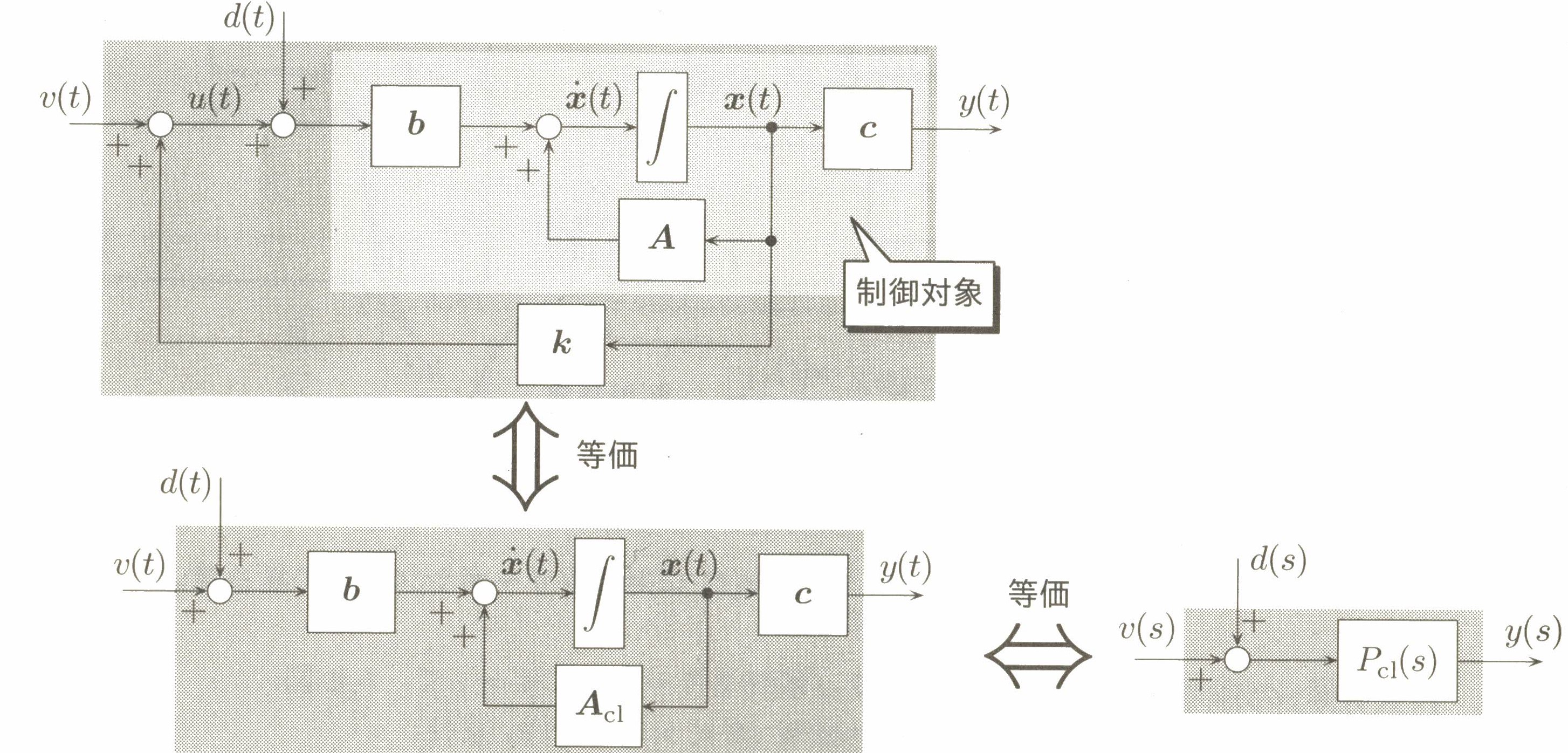
Figure 5.2
state feedback:
Theorem. Internal Model Principle
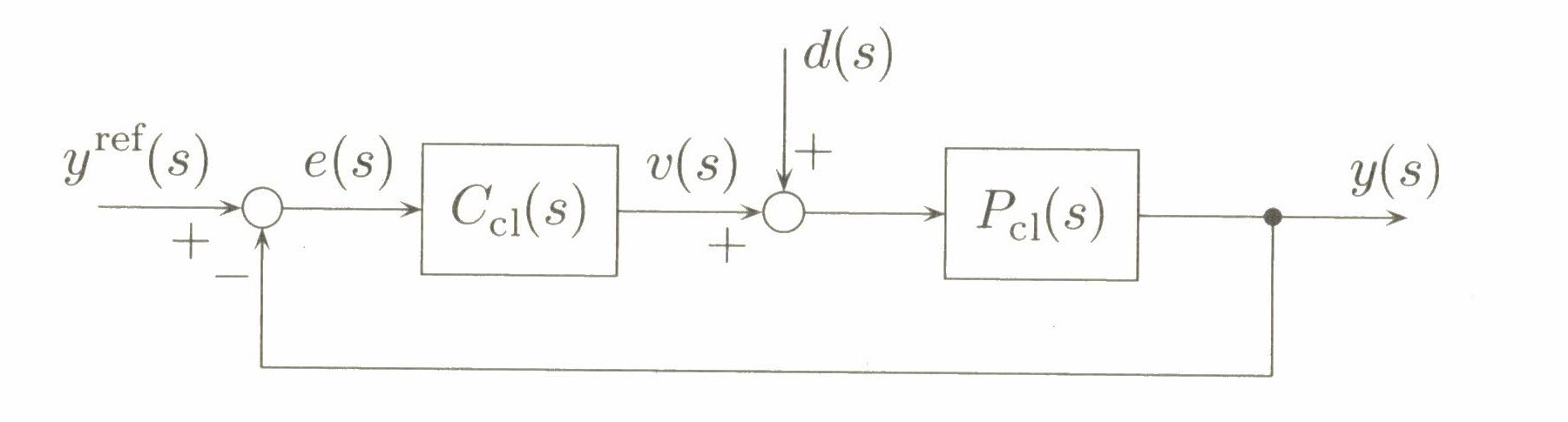
Figure 5.3 feedback control system
Reference and disturbance are step signal:
Decompose and in Num and Den:
are the solutions of , if all of the roots are zero, the feedback control system in Figure 5.3 is Internal stable .
If there are no cancellations of Num and Den in Equation (5.27), is:
There is stationary error in Equation (5.29). Accordingly, modify construction of controller transfer function as:
Internal model principle [ref] :
Condition
: reference and disturbance are step signal
Target
: With step target
, input disturbance
, steady-state deviation is zero (
)
Necessary and sufficient condition
:
1. Feedback control system in figure 5.3 is internal stable.
2. Transfer function
has no zeros at origin
.
3. Transfer function
has at least one integrator
.
Further [ref] [note] :
Condition
: reference and disturbance are
normal signals
other than step ones.
Using
generating polynomial
instead of integrator (actually it's a differentiator) in the denominator of
, see
[note]
.
5.2.2 状態フィードバック形式の積分型コントローラの設計
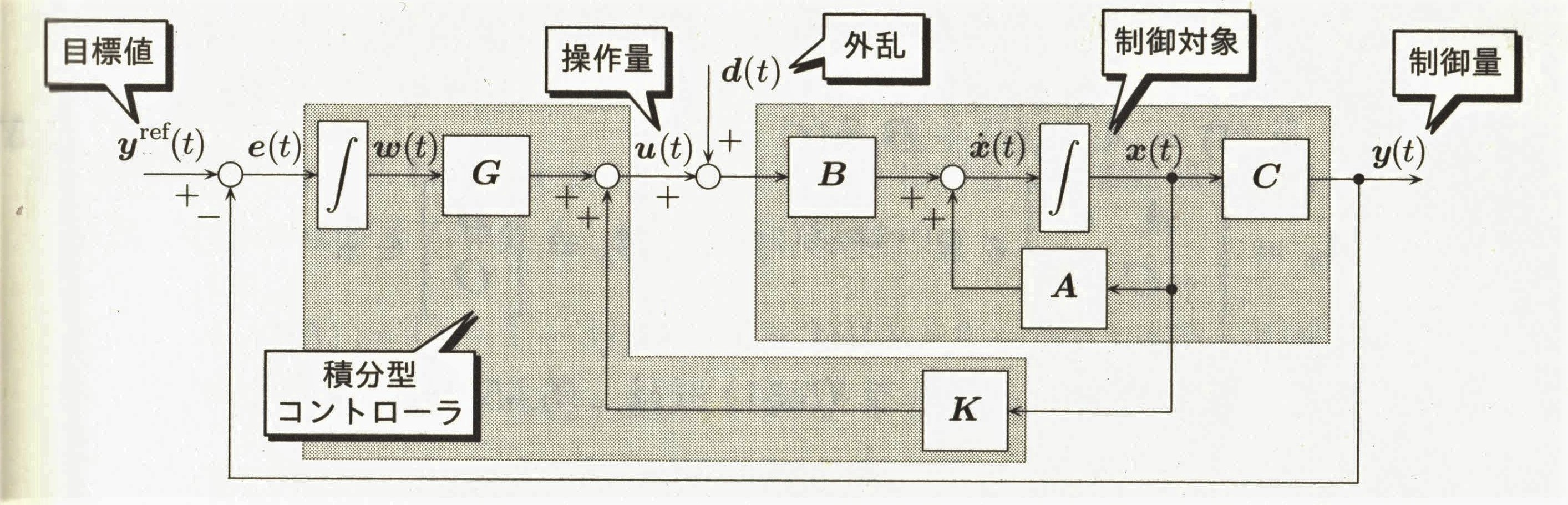
Figure 5.5 Integrator controller based servo control method
For system as (p2):
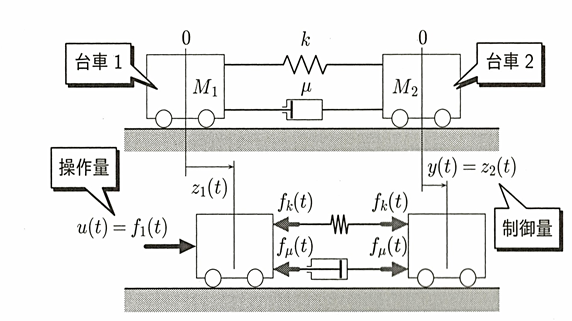
Figure 5.6 Two-cart inertial system
In a view of cart #1 state, a state feedback for cart #1 and I-PD controller for cart #2 is designed as:
which can be rewritten in 状態フィードバック形式( state variable feedback ) [ref] の積分型コントローラ as:
State feedback style integrator controller: